De los axiomas de los reales, éste es el que nos faltaba. A diferencia de los demás axiomas que tiene que ver más con propiedades algebraicas aplicables a diversos campos, éste es realmente característico de los reales.
¿Qué establece?
 Además:  |  Es decir:  |
Su importancia
1) Este axioma es característico de los números reales. Los racionales por ejemplo, no lo cumplen:
1) Este axioma es característico de los números reales. Los racionales por ejemplo, no lo cumplen:
Sea
 |  , pues al menos  .Además, por ejemplo, 2 es una cota superior de  .Sin embargo, no existe  . |
Es decir, no existe un racional que sea la mínima de todas las cotas superiores.
| |
Observe que:
Todos los racionales que son cotas superiores de son mayores que  ,pero a la vez existen racionales tan cerca de como se quiera. | |
2) Este axioma es necesario para establecer la existencia de los números irracionales y por consecuencia para completar los números reales. En análisis se llegan a construir como límites de sucesiones de racionales.
3) Con este axioma es posible atribuir a los números reales la propiedad de continuidad, es decir, de poder establecer una correspondencia biunívoca entre los reales y los puntos de una recta. Un punto de la recta corresponde a un racional o a un irracional.
3) Con este axioma es posible atribuir a los números reales la propiedad de continuidad, es decir, de poder establecer una correspondencia biunívoca entre los reales y los puntos de una recta. Un punto de la recta corresponde a un racional o a un irracional.
4) De una manera coloquial, se puede decir que este axioma garantiza que los reales llenan toda la recta. No obstante que entre cada dos racionales existe una infinidad de ellos, siempre es posible encontrar una infinidad (de mayor cardinalidad) de puntos que no corresponden a números racionales, esos precisamente, serán irracionales.
5) En temas de Continuidad en Cálculo 1, es de suma importancia para demostrar teoremas de gran trascendencia y similarmente para construir el concepto de función integrable, entre otros que podríamos mencionar.
Dos aclaraciones
1) Proposición. Si un conjunto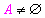 posee un supremo, éste es único.Dem:
Sean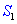
y 
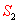supremos de 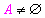(acotado superiormente).
Por el inciso b) de la definición tenemos que:
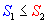y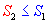 
, entonces 
.
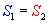1) Proposición. Si un conjunto
posee un supremo, éste es único.Dem:Sean
y supremos de (acotado superiormente). Por el inciso b) de la definición tenemos que:
y , entonces .
2) Se pueden formular definiciones similares para un conjunto 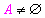pero acotado inferiormente y en este caso se llamaría 
(ínfimo de )
pero acotado inferiormente y en este caso se llamaría 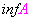(ínfimo de )
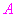0 comentarios:
Publicar un comentario