LOS NÚMEROS REALES

En matemáticas, un número real es un valor que representa una cantidad a lo largo de una línea continua. Los números reales incluyen todos los números racionales , tales como el número entero -5 y la fracción 4/3 , y todos los números irracionales como √ 2 ( 1,41421356 ... la raíz cuadrada de dos , un número algebraico irracional ) y π ( 3,14159265 ... , un número trascendental ) . Los números reales pueden ser considerados como puntos en una línea infinitamente larga llamada la línea de números o la línea real, donde los puntos correspondientes a los números enteros son equidistantes . Cualquier número real puede ser determinada por una representación decimal posiblemente infinita , como la de 8.632 , donde cada dígito consecutivo se mide en unidades de una décima parte del tamaño de la anterior . La línea real puede ser pensado como una parte del plano complejo , y correspondientemente , números complejos incluyen números reales como un caso especial .

Estas descripciones de los números reales no son lo suficientemente rigurosos para los estándares modernos de la matemática pura . El descubrimiento de una definición adecuada riguroso de los números reales - de hecho , la idea de que era necesaria una mejor definición - fue uno de los acontecimientos más importantes de las matemáticas del siglo 19 . La definición axiomática Actualmente estándar es que los números reales son la única Arquímedes complete el campo totalmente ordenado (R , +, · , < ) , hasta el isomorfismo , [ 1 ] mientras que las definiciones constructivas populares de números reales incluyen declarar como clases de equivalencia de secuencias de Cauchy de los números racionales , cortaduras de Dedekind , o ciertas " representaciones decimales infinitos " , junto con las interpretaciones precisas de las operaciones aritméticas y la relación de orden . Estas definiciones son equivalentes en el ámbito de la matemática clásica .
Los reales son incontables , es decir, mientras que tanto el conjunto de todos los números naturales y el conjunto de todos los números reales son conjuntos infinitos , no puede haber uno - a-uno la función de los números reales a los números naturales : la cardinalidad de la conjunto de todos los números reales ( denotado \ mathfrak cy llamado cardinalidad del continuo ) es estrictamente mayor que la cardinalidad del conjunto de los números naturales ( denotado \ aleph_0 ) . La afirmación de que no hay ningún subconjunto de los reales con cardinal estrictamente mayor que \ aleph_0 y estrictamente más pequeño que \ mathfrak c es conocida como la hipótesis del continuo . Se sabe que ni demostrable ni refutable usando los axiomas de la teoría de conjuntos de Zermelo - Fraenkel , la base estándar de las matemáticas modernas , proporcionado la teoría de conjuntos ZF es consistente .

Los números reales se expresan con fracciones decimales que tienen una secuencia infinita de dígitos a la derecha de la coma decimal, como por ejemplo 324,8232. Frecuentemente también se subrepresentan con tres puntos consecutivos al final (324,823211247…), lo que significaría que aún faltan más dígitos decimales, pero que se consideran sin importancia.

Las medidas en las ciencias físicas son siempre una aproximación a un número real. No sólo es más conciso escribirlos con forma de fracción decimal (es decir,números racionales que pueden ser escritos como proporciones, con un denominador exacto) sino que, en cualquier caso, cunde íntegramente el concepto y significado del número real. En el análisis matemático los números reales son objeto principal de estudio. Puede decirse que los números reales son la herramienta de trabajo de las matemáticas de la continuidad, como el cálculo y el análisis matemático, mientras que los números enteros lo son de las matemáticas discretas, en las que está ausente la continuidad.

Se dice que un número real es recursivo si sus dígitos se pueden expresar por un algoritmo recursivo. Un número no-recursivo es aquél que es imposible de especificar explícitamente. Aun así, la escuela rusa de constructivismo supone que todos los números reales son recursivos.

Los ordenadores sólo pueden aproximarse a los números reales por números racionales; de todas maneras, algunos programas de ordenador pueden tratar un número real de manera exacta usando su definición algebraica (por ejemplo, "") en vez de su respectiva aproximación decimal.

Los matemáticos usan el símbolo  (o, de otra forma, 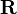, la letra "R" en negrita) para representar el conjunto de todos los números reales.

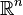La notación matemática  se refiere a un espacio de  dimensiones de los números reales; por ejemplo, un valor  consiste de tres números reales y determina un lugar en un espacio de tres dimensiones.

En matemática, la palabra "real" se usa como adjetivo, con el significado de que el campo subyacente es el campo de los números reales. Por ejemplo, matriz real, polinomio real, y Álgebra de Lie real.