TRANSITIVIDAD

Una relación binaria se puede representar como pares ordenados, mediante una matriz de adyacencia o mediante un grafo. Para el caso de una relación transitiva, cada una de estas representaciones tiene características especiales:

• Como pares ordenados, 

• Como matriz de adyacencia , la matriz es tal que 

• Como grafo, cada vez que desde un nodo 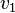 se pueda llegar a otro , pasando primero por un nodo intermedio 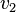, entonces también existirá la arista .

a

Una relación binaria  sobre un conjunto  es transitiva cuando se cumple: siempre que un elemento se relaciona con otro y éste último con un tercero, entonces el primero se relaciona con el tercero.

Esto es:

Dado el conjunto A y una relación R, esta relación es transitiva si: a R b y b R c se cumple a R c.

La propiedad anterior se conoce como transitividad.

Así por ejemplo dado el conjunto N de los números naturales y la relación de orden "menor o igual que" vemos que es transitiva:

Así, puesto que:

En general las relaciones de orden (ser menor, mayor, igual, menor o igual, mayor o igual) son transitivas.

Tomando de nuevo el conjunto de los números naturales, y la relación divide a:

Para todo valor a, b, c numero natural: si a divide a b y b divide a c entonces a divide a c

Dado que 3|12 (3 divide a 12) y 12|48 (12 divide a 48), la transitividad establece que 3|48 (3 divide a 48).

Sin embargo, no todas las relaciones binarias son transitivas. La relación "no es subconjunto" no es transitiva. Por ejemplo, si X = {1,2,3}, Y={2,3,4,5}, Z={1,2,3,4}. Entonces

Se cumple  y  pero no se cumple  puesto que  es subconjunto de .

Otro ejemplo de relación binaria que no es transitiva es "ser la mitad de": 5 es la mitad de 10 y 10 es la mitad de 20, pero 5 no es la mitad de 20.